The amount of money that must be invested today in order to realize a certain value in the future is present value (PV), which is the current price of a claim on a single payment or a series of payments due and payable at some specific future date or dates. The present value formula expresses how much must currently be paid for a claim to all of a bond’s promised future cash flows. The process of computing present value is discounting and the discount rate is the interest rate at which expected future cash flows are discounted.
There are two fundamental properties of present value:
- For a given value at a specified time in the future, the higher the discount rate applied, the lower the present value – the higher the rate earned on any sum invested today, the less that has to be invested; and
- For a given discount rate, the longer it takes to receive the future value, the lower its present value – the further into the future cash flows are to be received, the more interest accumulates due to the compounding of interest (interest-on-interest).
The two variable that are required to price any bond are:
- An estimate of the expected future cash flows (i.e., interest payments and redemption value).
- An estimate of the appropriate required yield.
A bond’s price is determined by adding the present value of the periodic coupon payments and the present value of the redemption value at maturity. The price of a zero-coupon bond is simply the present value of its redemption value, since it does not make any periodic coupon payments.
The price of a bond changes:
- When its required yield changes due to:
- A change in the credit quality of the issuer;
- A change in the bond’s liquidity;
- A change in the yield on comparable bonds; or
- Changes due to a change in relevant tax regulations.
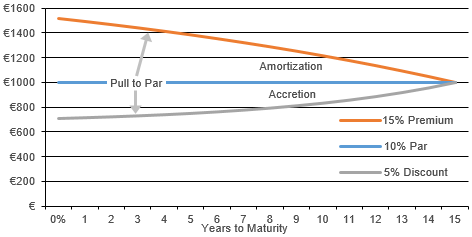
- Without any change in the required yield of a premium or discount bond that is moving toward its maturity.
| Price Path of Par, Premium and Discount Bonds (“Pull to Par”) |
 Source:
|

Leave A Comment
You must be logged in to post a comment.