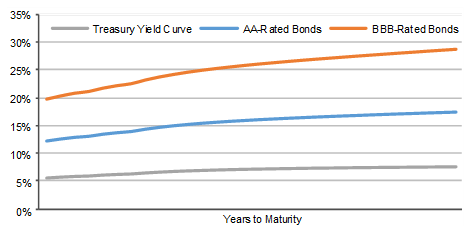
The difference in the required yield of a financial instrument relative to its benchmark is a yield spread, it reflecting the difference in the creditworthiness of an issue and/or its liquidity relative to the benchmark. In determining yield spreads, the credit risk and liquidity risk of the respective bonds relative to the benchmark are the principal factors. If the benchmark is a government yield curve, it is a government spread (G-spread); if the benchmark is the swap yield curve, it is an interpolated spread (I-spread).
| The US Yield Curve and Yield Spreads (Example) |
 Source:
|
The Z-spread is the basis point spread added to the spot rates along the benchmark yield curve – either the government yield curve or swap yield curve – to make the present value of a bond equal to its price. It is the spread that an investor would realize over the entire yield curve if the bond is held to maturity. Using the z-spread, the price of a bond can be calculated, where P is bond price, C is periodic coupon, n the number of coupon periods per year, z the benchmark spot rate, and Z the Z-spread:
P = (C1/(1 + z1 + Z)1 + (C1/(1 + z2 + Z)2 + … (C1 + F)/(1 + zn + Z)n
An option-adjusted spread (OAS) is the spread of a bond with an embedded option, such as a callable or puttable bond, over or below the benchmark spot rate of an option-free straight bond (the Z-spread), respectively, used to measure the relative risk of instruments with embedded options on a risk-adjusted basis. The OAS is positive for callable bonds and most mortgage-backed and asset-backed securities, because the option creates risks for the bondholder – the Z-spread is greater than OAS – and is negative for puttable bonds, because the option reduces price risk for investors and provides the bondholders an opportunity to profit from it – the Z-spread is lower than the OAS. Therefore:
Callable Bond OAS = Z-Spread + Call Option Value
and
Puttable Bond OAS = Z-Spread – Put Option Value

Leave A Comment
You must be logged in to post a comment.